(%i1) Mathe Q1: Wachstum & Wachstumsprozesse

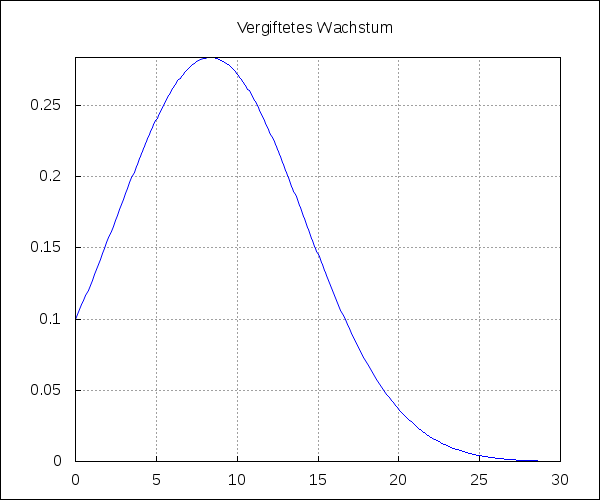
(%i2) Vergiftetes Wachstum

(%i3) (1)

(%i4) f(0) = 0.1 (Warum?)

(%i5) f(t) = 0.1 * %e^(0.25*t - 0.5 * c*t^2) und f(5) = 24

(%i6) -> 0.24 = 0.1 * %e^(0.25*5 - 0.5 * c * 25) -> 2.40 = %e^(0.25*5 - 0.5 * c * 25)

(%i7) log(2.40) = (0.25*5 - 12.5 * c) -> 12.5 * c = 
(0.25*5 - log(2.40) ) -> c = (0.25*5 - log(2.40) ) / 12.5

(%i8) (0.25*5 - log(2.40) ) / 12.5;
(%o8)                         0.02996250101168801

(%i9) ev(%,numer);
(%o9)                         0.02996250101168801

(%i10) d. h. c = 0.02996 = 0.03

(%i11) f(t) := 0.1 * %e^(0.25 * t - 0.015*t*t);
                                     0.25 t - 0.015 t t
(%o11)                 f(t) := 0.1 %e

(%i12) (2)

(%i13) _f_ : 0.1 * %e^(0.25 * t - 0.015*t*t);
                                                  2
                                  0.25 t - 0.015 t
(%o13)                      0.1 %e

(%i14) draw2d(explicit(_f_,t,0,30),title = Vergiftetes Wachstum,
xaxis = true,yaxis = true,grid = true)

(%i15) (3)

(%i16) maximale Anzahl = HP von f(t)

(%i17) diff(f(t),t);
                                                          2
                                          0.25 t - 0.015 t
(%o17)              0.1 (0.25 - 0.03 t) %e

(%i18) diff(80 - 80 * %e^(-0.05*t),t);
                                      - 0.05 t
(%o18)                          4.0 %e

(%i19) d. h. 0.25 - 0.03 t = 0 -> t = 0.25 / 0.03 = 8.33334

(%i20) f(8.333333334);
(%o20)                        0.2833936307694168

(%i21) HP(8.333334| 0.2834)

(%i22) (4) maximale Zunahme/maximale Abnahme = WST!

(%i23) diff(f(t),t,2);
                                              2                           2
                          2   0.25 t - 0.015 t            0.25 t - 0.015 t
(%o23) 0.1 (0.25 - 0.03 t)  %e                  - 0.003 %e

(%i24) WST falls 325 - 150 * t + 9 * t^2 = 0

(%i25) solve(325 - 150 * t + 9 * t^2 = 0,t);
                        10 sqrt(3) - 25      25 + 10 sqrt(3)
(%o25)           [t = - ---------------, t = ---------------]
                               3                    3

(%i26) ev(%,numer);
(%o26)          [t = 2.559830641437076, t = 14.10683602522959]

(%i27) max. Zunahme nach t = 2.56 Tagen, max. Abnahme nach t = 14.107 Tagen