(%i1) Mathe Q1: Wachstum & Wachstumsprozesse

(%i2) Logistisches Wachstum

(%i3) (1)

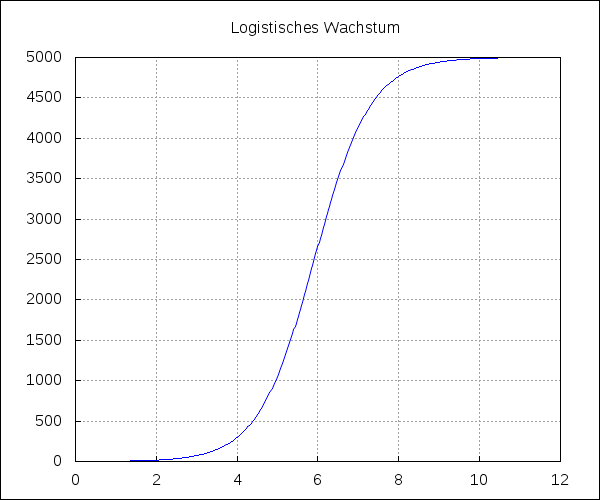
(%i4) Ausbreitung zunaechst exponentiell, danach asymptotisch gegen die Saettigungsgrenze G = 5000

(%i5) (2)

(%i6) f(0) = 1 = G / (1 + b) -> b = G - 1 = 4999 

(%i7) Wachstumskonstante k: f(4) = 300 = 5000 / (1 + 4999 * %e^(-k*4*5000)

(%i8) -> (1 + 4999 * %e^(-k*4*5000) = 50 / 3 -> 4999 * %e^(-k*4*5000) = 47 / 3

(%i9) -> %e^(-k*4*5000) = 0.003134 -> -k * 20000 = log(0.003134)

(%i10) -> k = log(0.003134) / (-20000) = 2.8827E-4

(%i11) f(t) := 5000 / (1 + 4999 * %e^(-1.44135 * t) );
                                         5000
(%o11)                  f(t) := ----------------------
                                       - 1.44135 t
                                4999 %e            + 1

(%i12) (3)

(%i13) Ansatz: 2500 = 5000 / (1 + 4999 * %e^(-1.44135 * t) )

(%i14) -> (1 + 4999 * %e^(-1.44135 * t) ) = 2 -> 4999 * %e^(-1.44135 * t) = 1

(%i15) -> %e^(-1.44135 * t) = 2 / 4999 -> -1.44135 * t = log(2 / 4999)

(%i16) -> t = log(1 / 4999) / (-1.44135) = 5.909

(%i17) d. h. t_D = 5,91 Wochen (mathematisch: Der Wendepunkt)

(%i18) (4) die mittlere Zunahme an Erkrankten

(%i19) f(8);
(%o19)                         4765.969950433076

(%i20) D. h. innerhalb von 8 Wochen von 1 auf ca. 4765.96 = 4766

(%i21) m = 4765 / 8 = (f(8) - 1) / 8 = 595.6212 = mittlere Zunahme


(%i22) _f_ : 5000 / (1 + 4999 * %e^(-1.44135 * t) );
                                     5000
(%o22)                      ----------------------
                                   - 1.44135 t
                            4999 %e            + 1

(%i23) draw2d(explicit(_f_,t,0,12),title = "Logistisches Wachstum",xaxis = true,yaxis = true,grid = true)