(%i1) Mathe Q1: Wachstum & Wachstumsprozesse

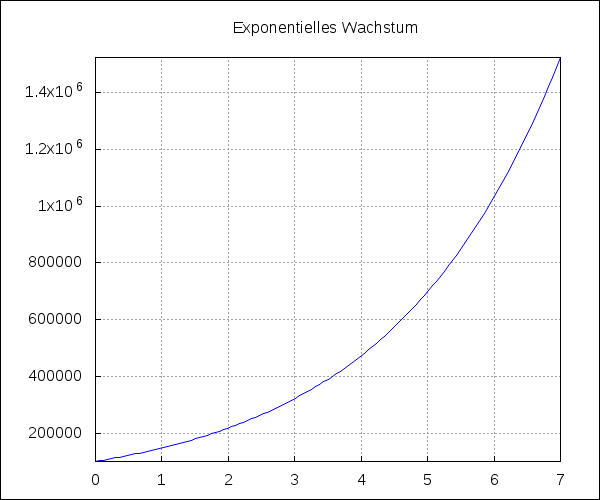
(%i2) Exponentielles Wachstum

(%i3) (1)

(%i4) a = 100 000 = g(0)

(%i5) g(5) = 700 000 = 100 000 * %e^(5*k) <-> 7 = %e^(5*k)

(%i6) 7 = %e^(5*k) <-> 5*k = log(7) <-> k = log(7) / 5

(%i7) log(7) / 5;
                                    log(7)
(%o7)                               ------
                                      5

(%i8) ev(%,numer);
(%o8)                         0.3891820298110626

(%i9) k = 0.389182 -> g(t) = 100 000 * %e^(0.389182*t)

(%i10) g(t) := 100000 * %e^(0.389182*t);
                                           0.389182 t
(%o10)                    g(t) := 100000 %e

(%i11) g(5);
(%o11)                         699999.8956612883

(%i12) (2)

(%i13) g(t) beschreibt die Anzahl der Keime in der Milch als Funktion der Zeit t

(%i14) (3)

(%i15) diff(g(t),t);
                                       0.389182 t
(%o15)                       38918.2 %e

(%i16) g'(t) beschreibt, wie schnell sich g(t) aendert

(%i17) (4)

(%i18) 1 000 000 = 100 000 * %e^(0.389182*t) <-> 10 = %e^(0.389182*t)

(%i19) 10 = %e^(0.389182*t) <-> 0.389182*t = log(10) <-> t = log(10)/0.389182

(%i20) log(10)/0.389182;
(%o20)                     2.56949190866998 log(10)

(%i21) ev(%,numer);
(%o21)                         5.916473765472314

(%i22) t = 5.916474 = 5.92 h, also nach knapp 6 Stunden

(%i23) (5)

(%i24) Ansatz: 2 = %e^(0.389182*t) <-> t = log(2)/0.389182

(%i25) log(2)/0.389182;
(%o25)                      2.56949190866998 log(2)

(%i26) ev(%,numer);
(%o26)                         1.781036071966189

(%i27) Also nach ca. 1.78 Stunden

(%i28) _f_ : 100000 * %e^(0.389182*t);
                                       0.389182 t
(%o28)                        100000 %e

(%i29) draw2d(explicit(_f_,t,0,7),
title = "Exponentielles Wachstum",xaxis = true,yaxis = true,grid = true)