(%i1) Mathe Q1: Wachstum & Wachstumsprozesse

(%i2) Beschraenktes Wachstum

(%i3) (1)

(%i4) f(0) = G + b = 80 + b = 0 -> b = -80

(%i5) Ausscheidung ueber die Niere: 5% -> k = 0.05

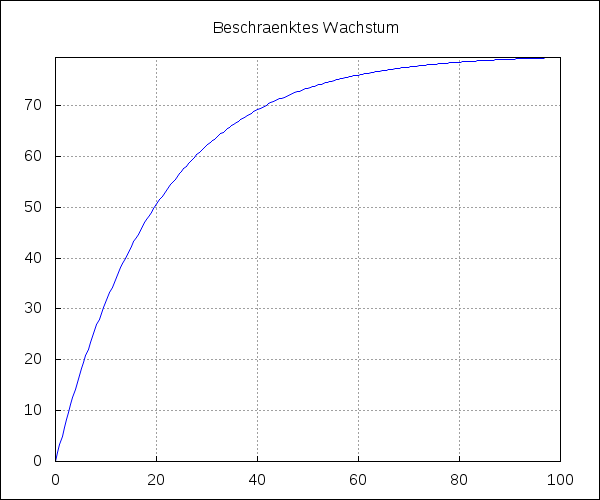
(%i6) f(t) := 80 - 80 * %e^(-0.05*t);
                                            - 0.05 t
(%o6)                     f(t) := 80 - 80 %e

(%i7) (2)

(%i8) f(t) beschreibt die Menge des Medikamentes 
im Blut in mg als Funktion der Zeit t in min

(%i9) (3)

(%i10) Betrachte die Ableitung f'(0)

(%i11) diff(80 - 80 * %e^(-0.05*t),t);
                                      - 0.05 t
(%o11)                          4.0 %e

(%i12) d. h. f'(0) = 4  -> Interpretation?

(%i13) (4)

(%i14) 0.9 * 80;
(%o14)                               72.0

(%i15) Ansatz: 72 = 80 - 80 * %e^(-0.05*t) ->
 80 * %e^(-0.05*t) = 8 -> %e^(-0.05*t) = 0.1 -> t = log(0.1) / (-0.05)

(%i16) log(0.1) / (-0.05);
(%o16)                         46.05170185988091

(%i17) d. h. nach 46,05 min hat man eine Konzentration von 72 mg im Blut

(%i18) _f_ : 80 - 80 * %e^(-0.05*t);
                                        - 0.05 t
(%o18)                        80 - 80 %e

(%i19) draw2d(explicit(_f_,t,0,100),title = "Beschraenktes Wachstum",
xaxis = true,yaxis = true,grid = true)